【原神】原神の理想ステータスの理論計算

今まで，いくつかの記事で理想ステータスの計算をしていました．
行き当たりばったりの計算で，理論としては完全に正しくない処方箋を用いたりもしていまして，モヤモヤが残っていました．
聖遺物の攻撃力実数メインの値を計算にいれて最低攻撃力を保証しつつ計算をしたり，少々煩雑な計算になっていました．
今回はもっとシンプルで美しい計算をしようと思います．

最適化の条件
ラグランジュの未定乗数法
スコア十分の場合
スコア不十分の場合
まとめ

最適化の条件

まず必要なステータスは基礎攻撃力 $B$ ，最終攻撃力 $a$ ，会心率 $c_r$ ，会心ダメージ $c_d$ ，ダメージバフ $D$ です．
基礎攻撃力に対する最終攻撃力の付加割合を攻撃力% $a_r$ としましょう．
つまり，攻撃力実数まで攻撃力%として繰り込んで計算していきます．
攻撃力の最小値を与えて最低攻撃力は保証していきます．
下付き添字 ${}_{\rm min}$ が各最小ステータスとします．
つまり，突破ステータスが会心率ならば $c_{r{\rm min}}=0.242$ みたいな感じです．
基礎攻撃力とダメージバフは定数とします．ダメバフをいじる場合は各々で期待値を計算して比較するということをします．

期待値に比例するものを $E$ とすれば，
$E(c_r,c_d,a_r)=(1+c_r c_d)a(1+D)=(1+c_r c_d)(1+a_r)B(1+D)$
です．そして拘束条件は聖遺物オプションの比率を参考に全合計ステータスを $S$ として，
$S(c_r,c_d,a_r)=2c_r+c_d+\frac{4}{3}a_r=S={\rm const.}$
となります．期待値を最適化の対象だけにして余分なものを取り除けば，ラグランジアンは
$L(c_r,c_d,a_r,\lambda)=(1+c_r c_d)(1+a_r)-\lambda(S(c_r,c_d,a_r)-S)$
$=(1+c_r c_d)(1+a_r)-\lambda(2c_r+c_d+\frac{4}{3}a_r-S)$
となります．わかりやすいように，変数を
$L(x,y,z,\lambda)=(1+x y)(1+z)-\lambda(2x+y+\frac{4}{3}z-S)$
としましょう．
これを，条件
$x_{\rm min} \leq x, y_{\rm min} \leq y, z_{\rm min} \leq z$
のもとで極大化しようというのが目的です．

ラグランジュの未定乗数法

まずこういう問題で最初にやることがラグランジュの未定乗数法です．
これにより極値の候補がわかります．
$\frac{\partial L}{\partial x}(x,y,z,\lambda) = y(1+z) - 2\lambda=0$
$\frac{\partial L}{\partial y}(x,y,z,\lambda) = x(1+z) - \lambda=0$
$\frac{\partial L}{\partial z}(x,y,z,\lambda) = 1+xy - \frac{4}{3}\lambda=0$
$\frac{\partial L}{\partial \lambda}(x,y,z,\lambda) = -(2x+y+\frac{4}{3}z-S)=0$
より，まず
$2x=y$
という会心率と会心ダメージ1:2がでてきます．
次に， $x\not = 0$ より，
$z=\frac{3}{4}(2x+\frac{1}{x})-1 \geq z_{\rm min}$
となります． $z$ は $x=\frac{1}{\sqrt{2}}=70.1\%$ で最小値
${\rm min}(z)=\frac{3}{\sqrt{2}}-1$
をとります．会心率70%を境にして，「理想」会心率が低くなればなるほど理想攻撃力が要求されることとなり，70%を超えたあたりからまた攻撃力を少しずつ増やしていくべきということになります．
最終的な計算結果で攻撃力なり会心率なりが設定した最小値を下回ることがなければ以降この計算が正しいということになります．
とりあえず拘束条件の式にいれれば
$S':= S+ \frac{4}{3}= 6x+\frac{1}{x}$
を得ます．これは

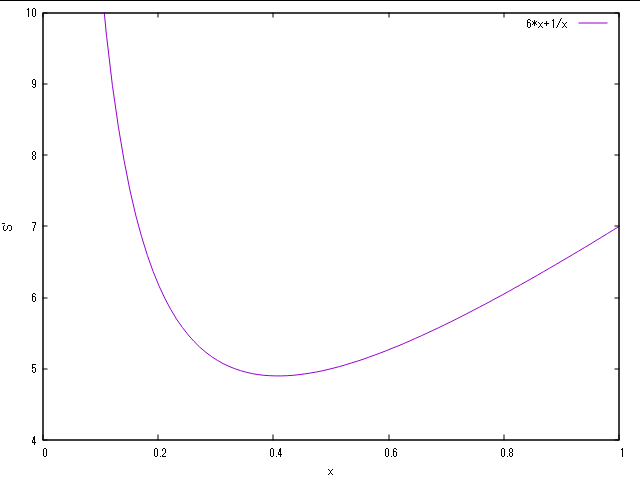
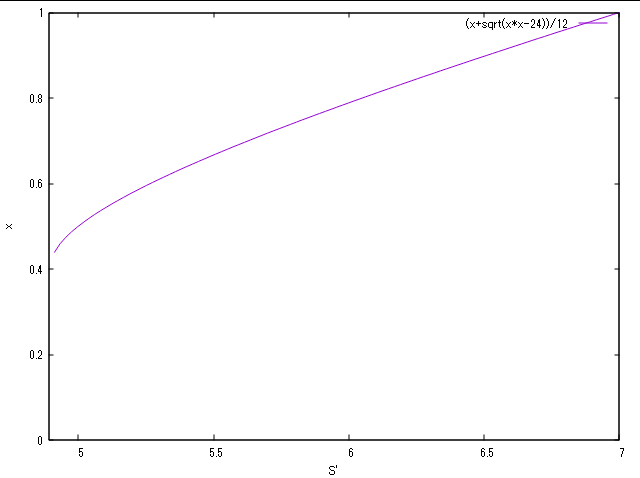
このようなグラフになり， $x=\frac{1}{\sqrt{6}}=40.8\%$ で最小値 $S'=2\sqrt{6}$ をとります．
この逆関数を与えたい(与えられたスコア $S'$ に対して最適会心率 $x$ を知りたい)ので，より高い会心率になる方を選択すれば，
$x=\frac{1}{12}(S'+\sqrt{S'^2-24})$
という逆関数を得ます．

一応計算しておくと，期待値すなわち $(1+xy)(1+z)$ は
$E(x,y,z)=\frac{3}{4}x(2x+\frac{1}{x})^2$
$E(S')=\frac{(72+(S'+\sqrt{S'^2-24})^2)^2}{576(S'+\sqrt{S'^2-24})}$
になります． $B(1+D)$ の因子は一旦省いておきます．

スコア十分の場合

$S' > 7$ すなわち理想会心率が100%に到達してしまった場合，攻撃力と会心ダメージにステータスを分配することになります．
$L(1,y,z,\lambda)=(1+y)(1+z)-\lambda(2+y+\frac{4}{3}z-S)$
を最大化すればよく，
$1+y=\frac{4}{3}(1+z)$
$z=\frac{3}{4}(y-\frac{1}{3})$
を満たせばいいというのはすぐにわかります．
このとき，
$S'=2y+3$
$y=\frac{1}{2}(S'-3)$
であり，期待値は
$E(1,y,z)=\frac{3}{4}(1+y)^2$
$E(S')=\frac{3}{16}(S'-1)^2$
となります．
ではスコア不十分 $0 \leq S' < 2\sqrt{6}$ の場合はどうでしょうか．

スコア不十分の場合

ここからは突破ステータスごとに話が変わってきます．

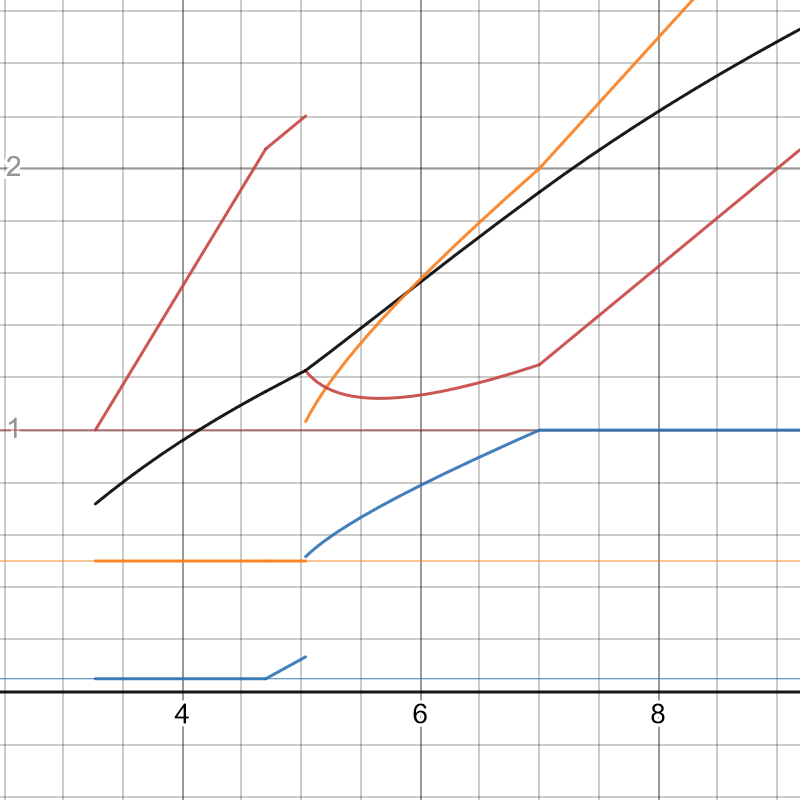
話を続ける前に一旦ここで今までの様子をグラフに表しておきます

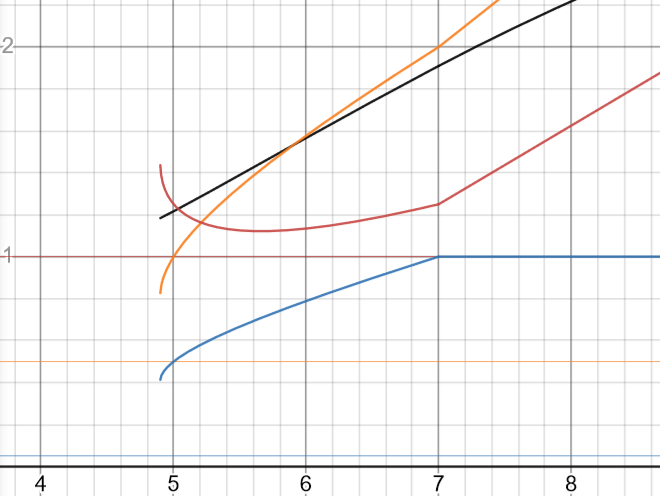
赤が攻撃力で青が会心率，橙が会心ダメージです．黒は期待値の自然対数です．
最小攻撃力を100%としています．突破ステータスは非会心系だと仮定しています．会心ステータスが上昇するとともに理想攻撃力が一度下がっているという振る舞いがわかるかと思います．

突破ステータスが会心系でない場合

スコアが最小付近のことから考えます．会心ダメージは0.5に固定してよさそうというのはいいと思います．
この場合結論から言えばすべて攻撃力に振るのが最適となります．会心率にスコアに対する増加関数だけ加えて期待値を計算すると，攻撃全振りのときから期待値が低くなるというのがわかります．
まず，攻撃全振りの場合は
$S'=2\times 0.05 + 0.5 + \frac{4}{3}(1+z)$
$z=\frac{3}{4}(S'-\frac{29}{15})$
$E(0.05,0.5,z)=\frac{41}{40}(1+z)=\frac{3}{4}\frac{41}{40}(S'-\frac{3}{5})$
となります．

一方， $\xi=\xi (S'-S_0)$
とおいて $x=0.05+\xi$ とすると
$S'=2\times (0.05 +\xi )+ 0.5 + \frac{4}{3}(1+z)$
$E(0.05+\xi ,0.5,z)=\frac{3}{4}(\frac{41}{40}+\frac{\xi}{2})(S'-\frac{3}{5}-2\xi )$
となります．
これが攻撃全振りの期待値を上回る条件は
$\xi(S'-S_0)<\frac{1}{2}(S'-4.7)$
となります．

仮に\xi(S'-S_0)が比例関数だと仮定した場合は $S'<4.7$ までは会心率に全く振らないほうが良いということになります．
ここからの最適化の方法はまだわかってないのですが，仮にそのような比例関数だと仮定して
$\xi(S'-S_0)=\frac{k}{2}(S'-4.7)$
( $k<1$ )だという形を仮定してみましょう．これを期待値に代入して $k$ で微分することにより，
$\frac{1}{4}(S'-4.7) \{ S'-\frac{3}{5}-k(S'-4.7) \} = (S'-4.7) \{ \frac{41}{40} +\frac{k}{4}(S'-4.7) \}$
$k=\frac{1}{2}$
ときれいな数が求まります．よって，線形であれば
$x=0.05+\xi(S'-S_0)=0.05+\frac{1}{4}(S'-4.7)$
がよいということがわかりました．このとき，
$z=2.075+\frac{3}{8}(S'-4.7)$
$E(S')=\frac{3}{64}(S'-4.7+\frac{41}{5})^2=\frac{3}{64}(S'+\frac{7}{2})^2$
ですね．つまり最低保証されている攻撃力が207.5%を上回る場合はこれではだめですが相当基礎攻撃力が低くない限りは大丈夫だと思うのでここの議論は省きます．

ここまでをまとめると，スコア $S'$ が4.7に満たない場合は攻撃力から盛っていき，最大で207.5%になります．
207.5%まで到達した場合，そこからは増えたスコアを会心:攻撃=2:3で分配していくのがよいということになります．

しかしひとつ気を付けなければならないことがあります．実は一番最初に計算した領域の期待値を上回る領域があるということです．
ラグランジュの未定乗数法は十分性が担保されているわけではないので極大の候補でしかありませんでした．
実際，
$\frac{3}{64}(S'+\frac{7}{2})^2 < \frac{(72+(S'+\sqrt{S'^2-24})^2)^2}{576(S'+\sqrt{S'^2-24})}$
を数値的に解くと
$S' > 5.0346...$
となります．つまりこのスコアまでは先ほど述べたようなスコア配分のままでいくのが最適ということになります．このときは
$x=\frac{1}{12}( 5.0346+\sqrt{ 5.0346^2-24})=0.516...$
となります．つまりさきほどの会心率の範囲は40.8%~ではなくて実は51.6%~だったんですね．
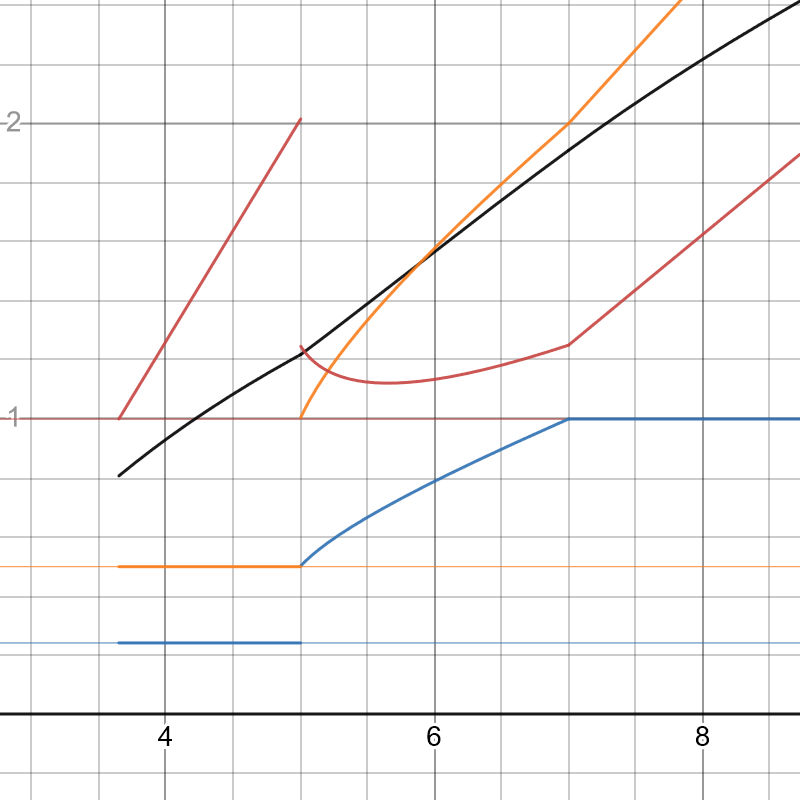
以上をまとめてグラフにするとこのようになります．

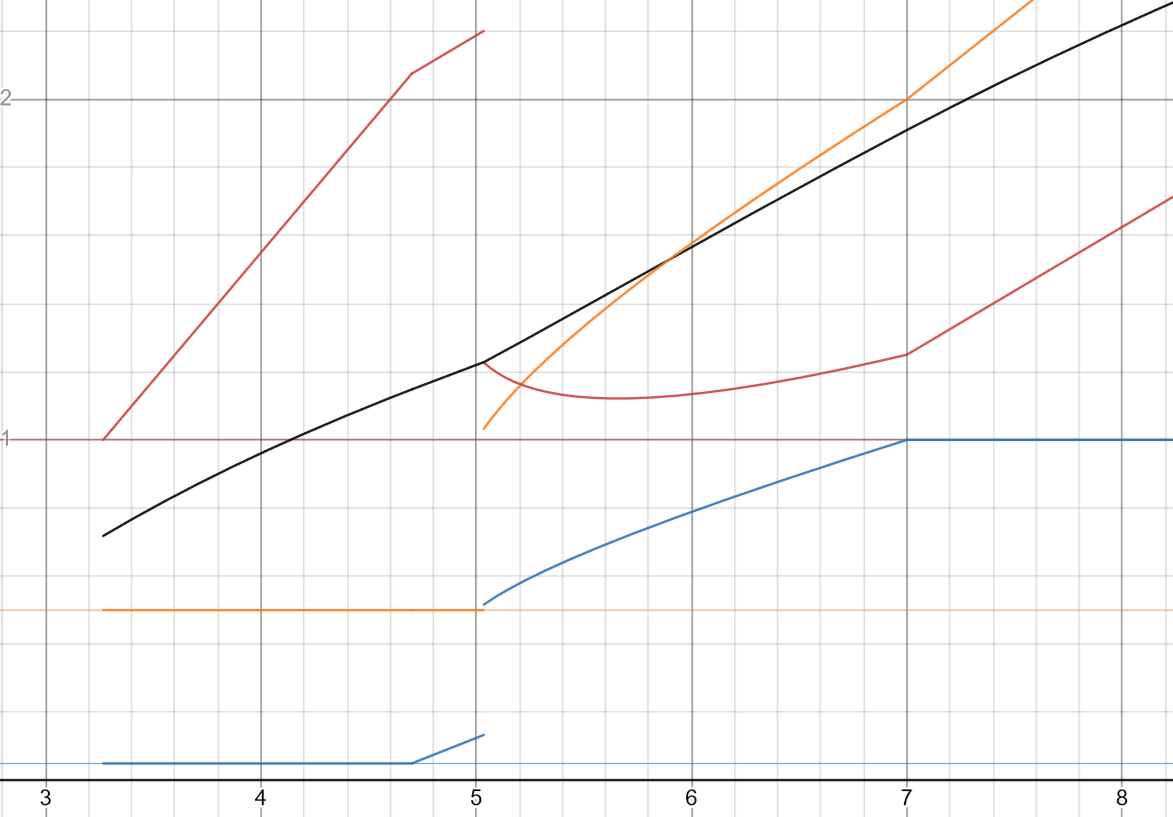
$S'_{\rm min}\leq S' < 4.7$ ， $4.7 \leq S' < 5.03$ ， $5.03 \leq S' < 7$ ， $7 \leq S'$ で場合わけされるんですね．

突破ステータスが会心率の場合

突破ステータスの場合，ほんの少しだけ話が変わってきます．というのも会心比率が最小の時点で1:2に近いため，
攻撃を稼ぎ続けても期待値が伸びやすいという傾向が予想されます．
攻撃振りは
$S'=2\times 0.242 + 0.5 + \frac{4}{3}(1+z)$
$z=\frac{3}{4}(S'-2.317373...)$
$E(0.242,0.5,z)=1.121(1+z)=1.121\times \frac{3}{4}(S'-0.984)$
となります．ここでグラフを書いてみると

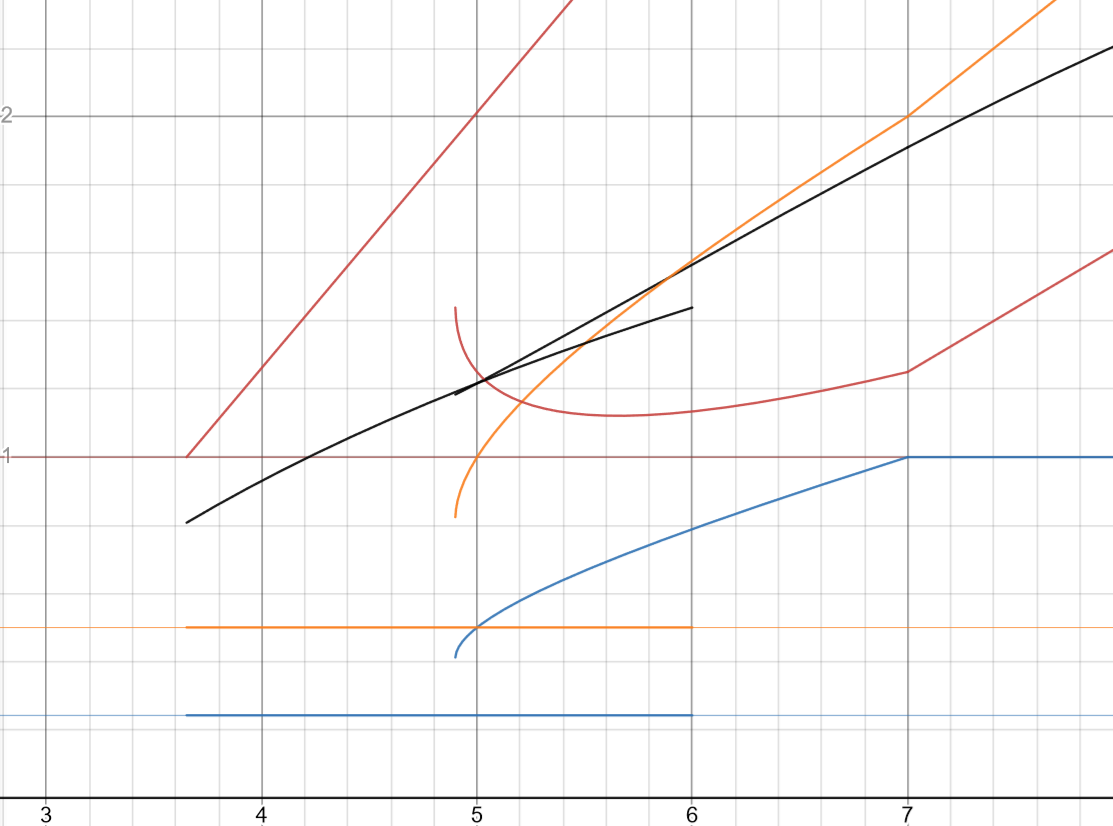
このようになっています．ここで一応会心率に少し割いた場合に期待値が上回ることがないのかを考えます．先ほどと同様の計算で，
$\xi=\xi (S'-S_0)$
$x=0.242+\xi$ とすると
$S'=2\times (0.242 +\xi )+ 0.5 + \frac{4}{3}(1+z)$
$E(0.242+\xi ,0.5,z)=\frac{3}{4}(1.121+\frac{\xi}{2})(S'-0.984-2\xi )$
となるので攻撃振りを上回る条件は
$\xi(S'-S_0)<\frac{1}{2}(S'-5.468)$
となります．グラフを見るに，もはやこの領域ではラグランジュの未定乗数法の最大候補が優勢ですのでこれを考える必要性はなさそうです．
ということで，ラグランジュの候補と攻撃振りが入れ替わる点を求めればよく，
$1.121\times \frac{3}{4}(S'-0.984)< \frac{(72+(S'+\sqrt{S'^2-24})^2)^2}{576(S'+\sqrt{S'^2-24})}$
を数値的に解くと
$S' > 5.00507...$
となります．このとき
$x=\frac{1}{12}( 5.00507+\sqrt{ 5.00507^2-24})=0.503...$
となり，今度は50.3%~になります．
このときの攻撃振りの値は $z=2.016$ になるのでスコアが低いうちは201.6%まで攻撃力に振りつづけ，そこからはラグランジュの未定乗数法に従ってステータス配分をするのがよいということになります．

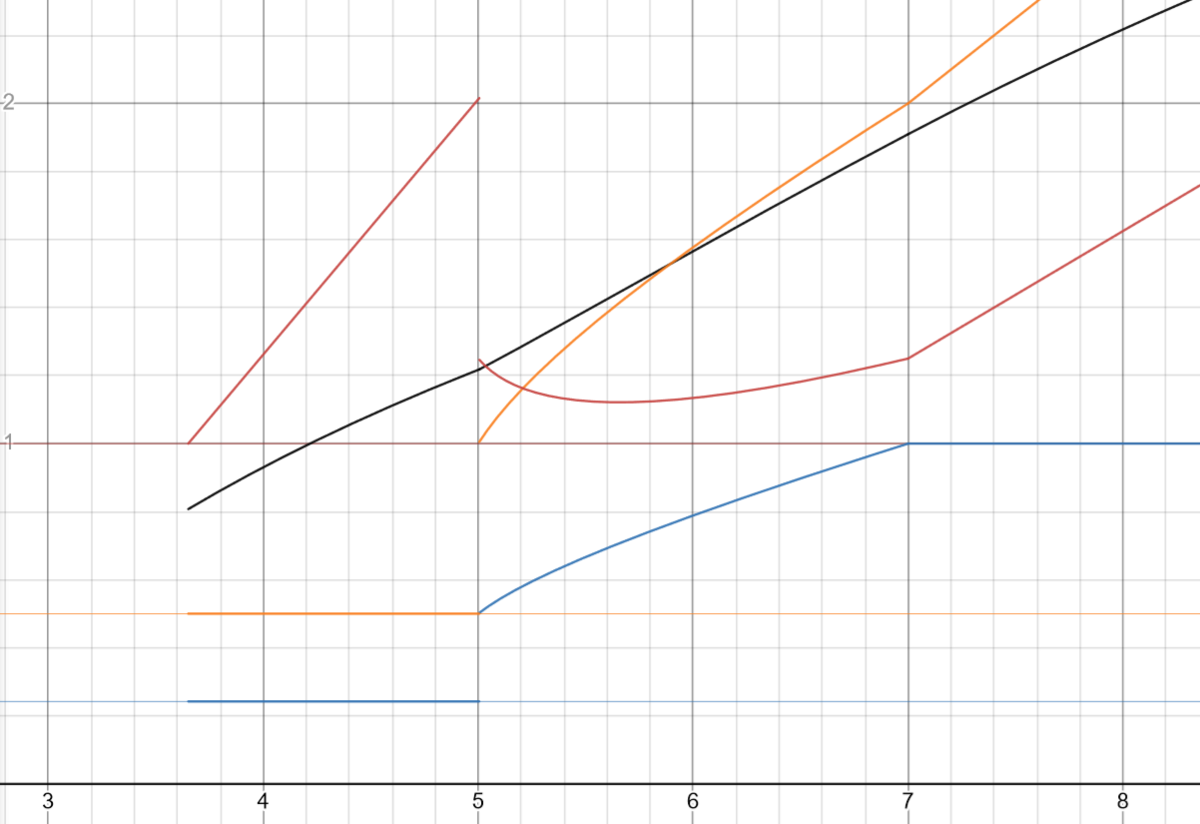
$S'_{\rm min}\leq S' < 5.01$ ， $5.01 \leq S' < 7$ ， $7 \leq S'$ とシンプルな場合わけになっています．

突破ステータスが会心ダメージのとき

今度は逆に高い会心ダメージに対して低すぎる会心率であって，非常にアンバランスとなった状態からはじまるので，
その高い会心ダメージについていくように会心率を盛ることで期待値が伸びやすく，
比較的早い段階で攻撃振りの伸びが悪くなってくることが予想されます．
攻撃全振りの場合は
$S'=2\times 0.05 + 0.884 + \frac{4}{3}(1+z)$
$z=\frac{3}{4}(S'-2.317373...)$
$E(0.05,0.884,z)=1.0442\times (1+z)=1.0442\times \frac{3}{4}(S'-0.984)$
となります．これから実際，グラフを書いてみると

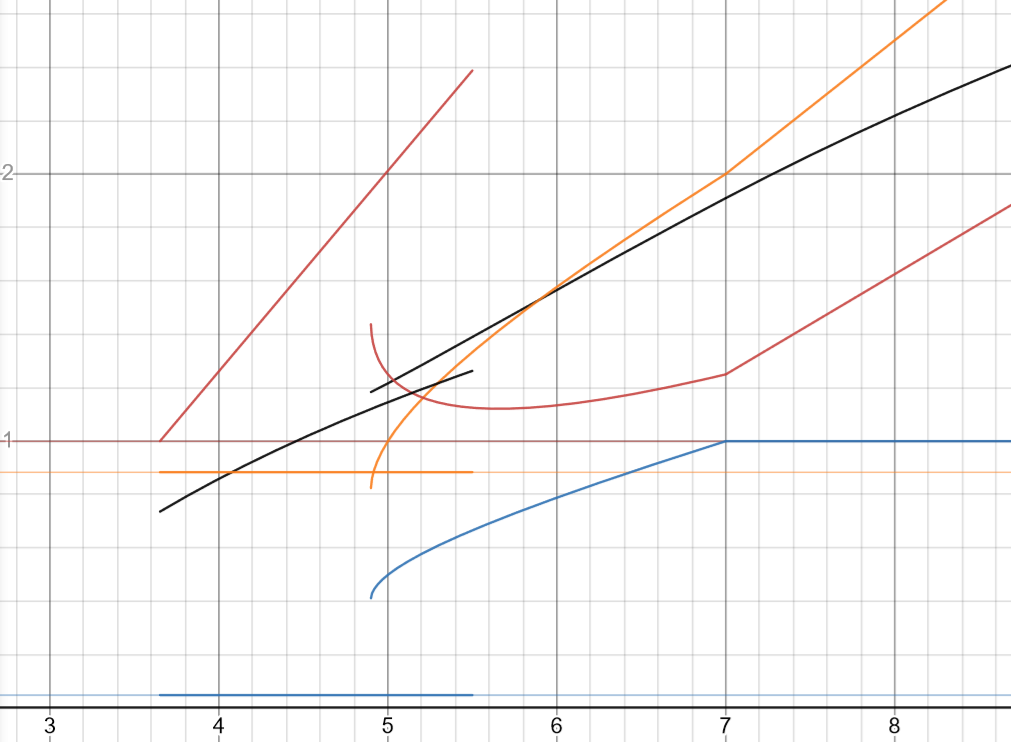
となっていて，攻撃振りの期待値が大きく下がっていることがわかると思います．
なので逆に会心率振りのほうから考えていきましょう．その場合，
$x=\frac{1}{2} \{ S'-0.884-\frac{4}{3}(1+z_{\rm min}) \}$
$E(S')=\{ 1+ 0.442\times \{ S'-0.884-\frac{4}{3}(1+z_{\rm min}) \}(1+z_{\rm min})$
となります．これを会心ダメージ÷2に達するまですなわち
$S'=1.768+\frac{4}{3}(1+z_{\rm min})$
まで続け，その後に攻撃力に振り続けるという場合，
$z=\frac{3}{4}(S'-3.101333...)$
で期待値は
$E(S')=1.390728\times \frac{3}{4}(S'-1.768)$

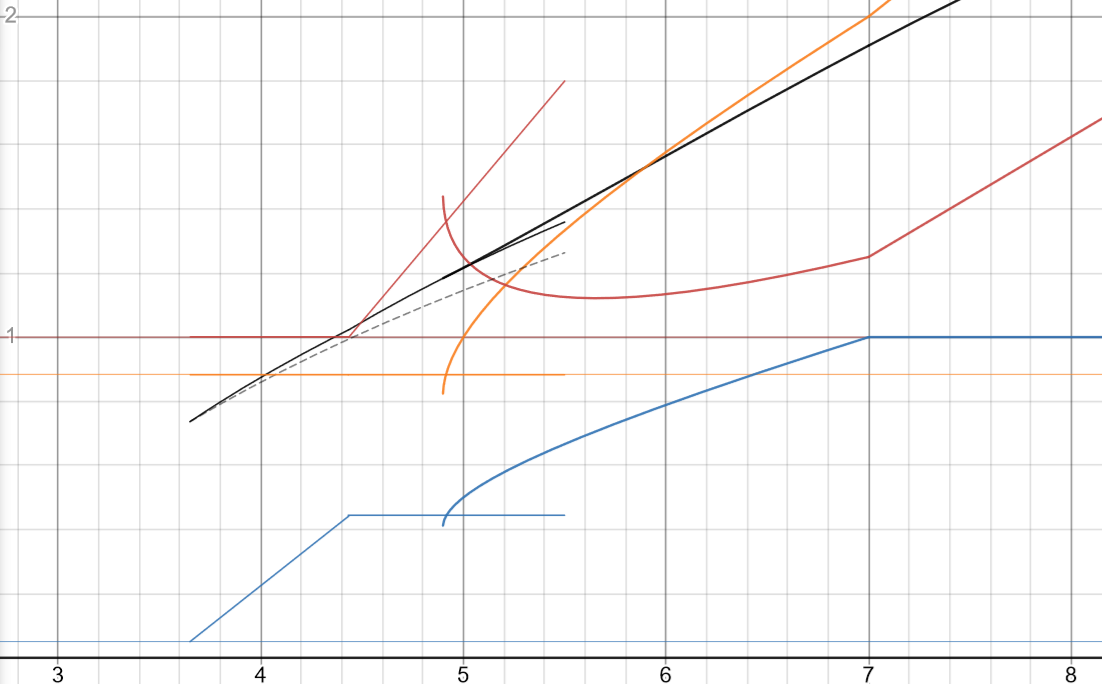
このようになりました．もちろんこれが最適解である保証はされてないのですが悪くはなさそうです．
求めるべきものはラグランジュ未定乗数法の候補との交点で，それは
$1.390728\times \frac{3}{4}(S'-1.768)< \frac{(72+(S'+\sqrt{S'^2-24})^2)^2}{576(S'+\sqrt{S'^2-24})}$
を数値的に解くと
$S' > 4.914443...$
となり，
$x=\frac{1}{12}( 4.91444+\sqrt{ 4.91444^2-24})=0.442...$
会心率は44.2%~になります．
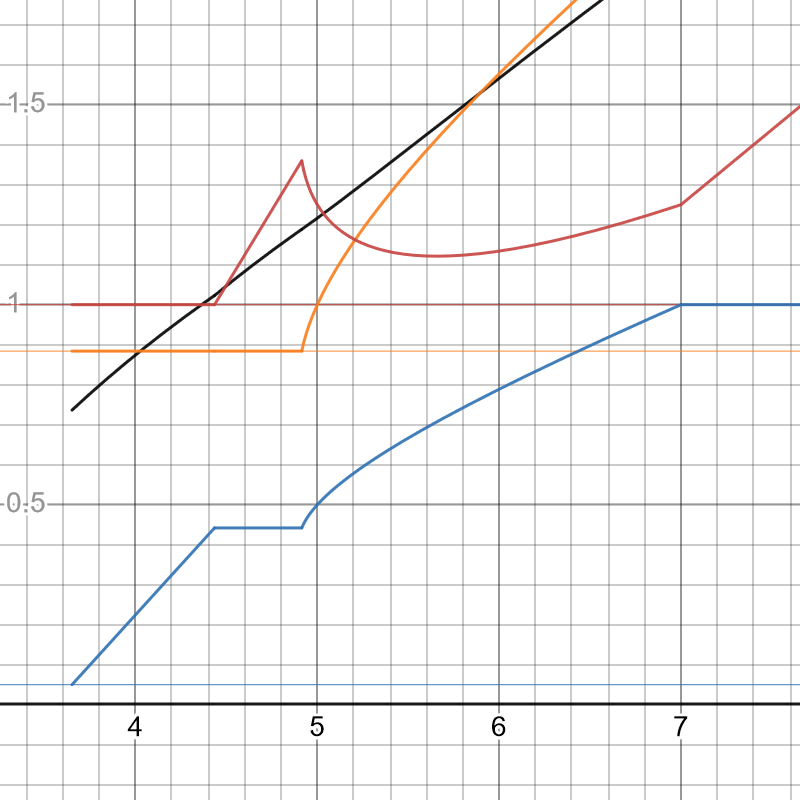
グラフは以下のようになります．

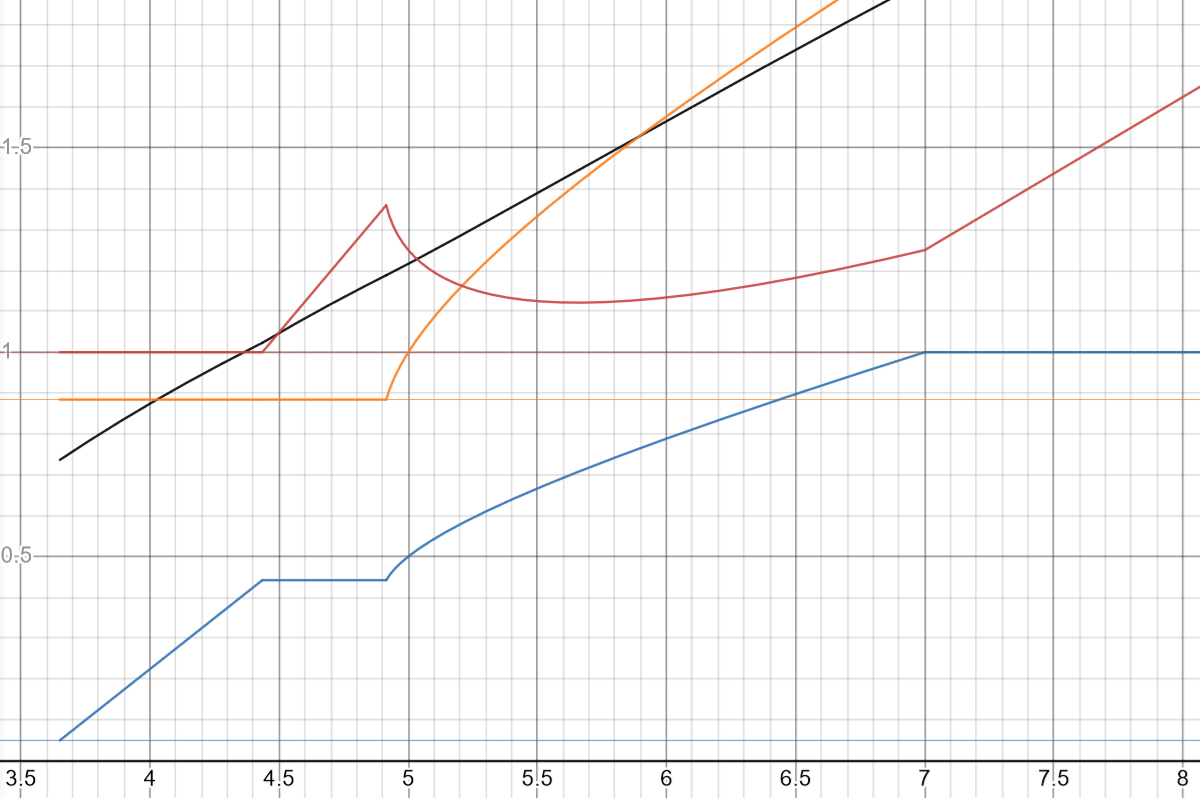
$S'_{\rm min}\leq S' < 1.768+\frac{4}{3}(1+z_{\rm min})$ ， $1.768+\frac{4}{3}(1+z_{\rm min}) \leq S' < 4.914$ ， $4.914 \leq S' < 7$ ， $7\leq S'$ という場合わけになっています．